北工大图形学

更新: 12/9/2025 字数: 0 字时长: 0 分钟

Introduction

图形学 (Computer Graphics) 是计算机科学的一个分支，主要研究如何使用计算机生成和处理图像。它涵盖了从基本的图形绘制到复杂的三维建模和渲染技术。

图形学严重依赖数学 (Graphics depends on mathematics)，图形学常用的数学工具有：

几何学 (Geometry)
线性代数 (Linear Algebra)
微积分 (Calculus)

Linear Algebra

这部分基本都是比较基础的知识，有关线代的内容可以参考我 Games101 中的笔记，该笔记还介绍到了第8节课才会介绍的齐次坐标 (Homogeneous Coordinates) 的内容，也可以一并了解一下。

Games101/Lec_1.md#review-of-linear-algebra

老师的 pdf 里还提到了基 (Basis) 的概念，指的是一组向量，通过线性组合可以表示空间中的任意向量。正交规范基 (Orthonormal Basis) 是指一组互相垂直且长度为 1 的基向量，比如 $(1, 0, 0)$ 、 $(0, 1, 0)$ 和 $(0, 0, 1)$ 。

这里再顺边标记一下一些常见数学名词的英文翻译：

向量 (Vector)
矩阵 (Matrix)
标量 (Scalar)
点积 (Dot Product)
叉积 (Cross Product)
行列式 (Determinant)
交换律 (Commutative Law)
结合律 (Associative Law)
分配律 (Distributive Law)
单位矩阵 (Identity Matrix)
逆矩阵 (Inverse Matrix)
转置矩阵 (Transpose Matrix)

可以通过代码来实现线代中的概念。使用 Point3f 类来表示三维空间中的点：

javakotlin

java

public class Point3f {
    public float x, y, z;

    public Point3f() {
        this(0, 0, 0);
    }

    public Point3f(float x, float y, float z) {
        this.x = x;
        this.y = y;
        this.z = z;
    }
}

kotlin

data class Point3f(var x: Float = 0f, var y: Float = 0f, var z: Float = 0f)

使用 Vector3f 类来表示三维空间中的向量：

javakotlin

java

public class Vector3f {
    public float x, y, z;

    public Vector3f() {
        this(0, 0, 0);
    }

    public Vector3f(float x, float y, float z) {
        this.x = x;
        this.y = y;
        this.z = z;
    }

    public float length() {
        return (float) Math.sqrt(x * x + y * y + z * z);
    }

    public Vector3f normal() { }
    public Vector3f dot(Vector3f v) { }
    public Vector3f cross(Vector3f v) { }
}

kotlin

data class Vector3f(var x: Float = 0f, var y: Float = 0f, var z: Float = 0f) {

    val length: Float
        get() = sqrt(x * x + y * y + z * z).toFloat()

    fun normal(): Vector3f { }
    fun dot(v: Vector3f): Float { }
    fun cross(v: Vector3f): Vector3f { }
}

Rasterization

将上述数学概念转换为屏幕上的像素，这个过程就叫做光栅化 (Rasterization) 。

线

在讲画线和画三角形之前，我们必须先理解插值 (Interpolation)。插值简单来说就是在已知两个点的情况下，计算出这两个点之间的某个点的值。

线形插值 (Linear Interpolation) 是最简单的一种插值方式，就是根据两个端点的某个属性，按照比例关系计算出中间点的属性值：

f (t) = f (A) + \frac{t - A}{B - A} \cdot (f (B) - f (A))

INFO

ppt 里没提到，但在更简单的 $t$ 在0到1的范围内，上面的公式可以简化为更直观的形式：

f (t) = f (A) * (1 - t) + f (B) * t

接下来讲解一下如何绘制一条线，ppt 值谈到了三种方法：

算法	原理	优点	缺点
Explicit Form	$y = m x + c$ 。循环 $x$ ，计算 $y$	概念上简单	在斜率 $m > 1$ 时会失效（线条不连续）； $x 1 < x 0$ 时也失效，需要更多的 if-else 判断，十分麻烦
Implicit Form	$d i s t a n c e ((x, y), l i n e) < 0.5$ 。通过两点确定一条直线，然后检查一个区域内的所有像素，看它离线的距离是否足够近。	适用性强	它画的是一条无限长的直线 (line)，而不是线段 (segment) ，实际使用中我们用 `x_min` 和 `x_max` 来限制
Parametric Form	$r = p + (q - p) * t$ 。循环 $t$ 从 $0.0$ 到 $1.0$	易于编码	ppt 中未提及

参数法 (Parametric Form) 是最优的，因为它不仅简单，而且完美地契合了插值。

ex:

kotlin

for (i in 0..1000) {
    val t = i / 1000.0 
    val point_r = point_p + (point_q - point_p) * t
    setPixel(round(point_r.x), round(point_r.y))
}

由于 Java 里不支持运算符重载等特性，必要时，我会使用 kotlin 来编写更贴合 ppt 中伪代码的示例。

填充三角形

现代图形学中万物皆为三角形，填充三角形是图形学中的基本操作。ppt 中提到了三种方法：

显式法 (Explicit Form / Raster Scan)
- 按 x 坐标（列）循环。对于每一个 x，计算出三角形在此处上边缘的 yMax 和下边缘的 yMin。然后填充 yMin 到 yMax 之间的所有像素。
- 插值操作非常复杂：为了计算三角形一点的颜色，在遍历每一列时，你需要计算该列所在直线和三角形上下两条边的交点的颜色，然后根据交点的 y 坐标进行插值；但要获得上下交点的颜色，又从上下交点各自所在边的端点进行插值。
隐式法 (Implicit Form / Half-Plane Test)
- 基于一个事实：一个点 P 如果在所有边的内侧，那它就在三角形内。在逆时针三角形中（A->B->C 逆时针排序），点在所有边的左侧即为在三角形内，顺时针同理点需在边右侧。
- 插值也很困难，难以做到颜色混合。
参数法 (Parametric Form / Barycentric)
- 三个权重 $α$ (alpha), $β$ (beta), $γ$ (gamma) 来表示三角形内的任意一点 P。
- $α$ 是 P 相对于 A 点的权重——离 A 越近, $α$ 越接近 $1.0$ ；在 BC 边上, $α$ 为 $0$ 。 $β$ 和 $γ$ 同理。
- 重要性质：
  - $α + β + γ = 1$
  - $α, β, γ >= 0$ 时，点 P 在三角形内
  - 当点在三角形内时， $α, β, γ$ 可以直接用作插值的权重
- 插值公式， $f$ 可以代表颜色、法线等属性： $f (P) = α * f (A) + β * f (B) + γ * f (C)$

同样，参数法是最推荐的：

kotlin

for (x in xMin until xMax) {
    for (y in yMin until yMax) {
            
        val alpha = distance(Point(x, y), BC) / distance(A, BC)
        val gamma = distance(Point(x, y), AB) / distance(C, AB)
        val beta = 1.0 - alpha - gamma
       
        if (alpha < 0.0 || beta < 0.0 || gamma < 0.0) {
            continue
        }

        val finalColour = colour(A) * alpha + 
                          colour(B) * beta + 
                          colour(C) * gamma 

        setColour(finalColour)
        setPixel(x, y)
    }
}

Geometric Modelling

描述世界

什么是建模？它是对世界的描述，回答三个问题：

物体在哪里 (where)
是什么 (what)
如何表现 (how)

如何去描述一个复杂的图形，比如一棵树？我们可以将复杂物体分解 (break into) 为更小的、简单的图元 (primitives) ，比如点，线，球体 (spheres)、圆柱体 (cylinders)、多边形 (polygons) 等。

如此一来，一棵树可以表述为：棕色圆柱体 + 绿色球体

通过构造实体几何 (CSG - Constructive Solid Geometry)，我们可以使用布尔运算 (Boolean Operations) 来组合简单图元，形成复杂物体，例如：

并集 (Union) ：A ∪ B
差集 (Subtraction) ：A - B
异或 (XOR) ：A ⊕ B

CSG_ex

值得一提的是，OpenGL 不支持高级的CSG操作（如差集），它只是把所有东西都画出来（即并集）。

万物皆为三角形

这是现代图形学的核心原则。

我们已经知道如何绘制填充的三角形，一个关键点是：任何多边形都可以被分解（三角化）成一组三角形。只要我们会画三角形，就能绘制任何填充的 2D 多边形 (Polygons)。

3D 多面体 (Polyhedra) 是由多个面 (faces) 组成的，每一个面本质上就是一个 2D 多边形，所以只要我们会画三角形，我们就能绘制任何 3D 多面体。

描述一个长方体，需要定义8个顶点，12 个三角形：

kotlin

val vertices: Array<IntArray> = arrayOf(
    intArrayOf(-1, -1, -1), // 顶点 0
    intArrayOf(-1, -1,  1), // 顶点 1
    intArrayOf(-1,  1, -1), // 顶点 2
    intArrayOf(-1,  1,  1), // 顶点 3
    intArrayOf( 1, -1, -1), // 顶点 4
    intArrayOf( 1, -1,  1), // 顶点 5
    intArrayOf( 1,  1, -1), // 顶点 6
    intArrayOf( 1,  1,  1)  // 顶点 7
)

val triangles: Array<IntArray> = arrayOf(
    intArrayOf(0, 1, 3),
    intArrayOf(0, 2, 4),
    intArrayOf(0, 1, 4),
    intArrayOf(1, 5, 7),
    intArrayOf(5, 4, 6),
    intArrayOf(2, 3, 7),
    intArrayOf(0, 3, 2),
    intArrayOf(2, 6, 4),
    intArrayOf(1, 4, 5),
    intArrayOf(1, 7, 3),
    intArrayOf(5, 6, 7),
    intArrayOf(2, 7, 6)
)

TIP

在指定这些三角形时，最好采用 CCW (逆时针) 顺序。

描述球形物体时，我们用面数非常多的多面体来近似圆形物体。

对于圆柱体，可以将其视为一个多边形的柱状体，底面和顶面是多边形，侧面是矩形。通过增加底面和顶面的边数，可以使圆柱体更接近真实的圆柱形状。

对于圆形，我们先讲解如何从球坐标 ( $ϕ$ , $θ$ ) 转换为笛卡尔坐标 (x, y, z) 的关键公式：

$x = r \sin (ϕ) \cos (θ)$

$y = r \sin (ϕ) \sin (θ)$

$z = r \cos (ϕ)$

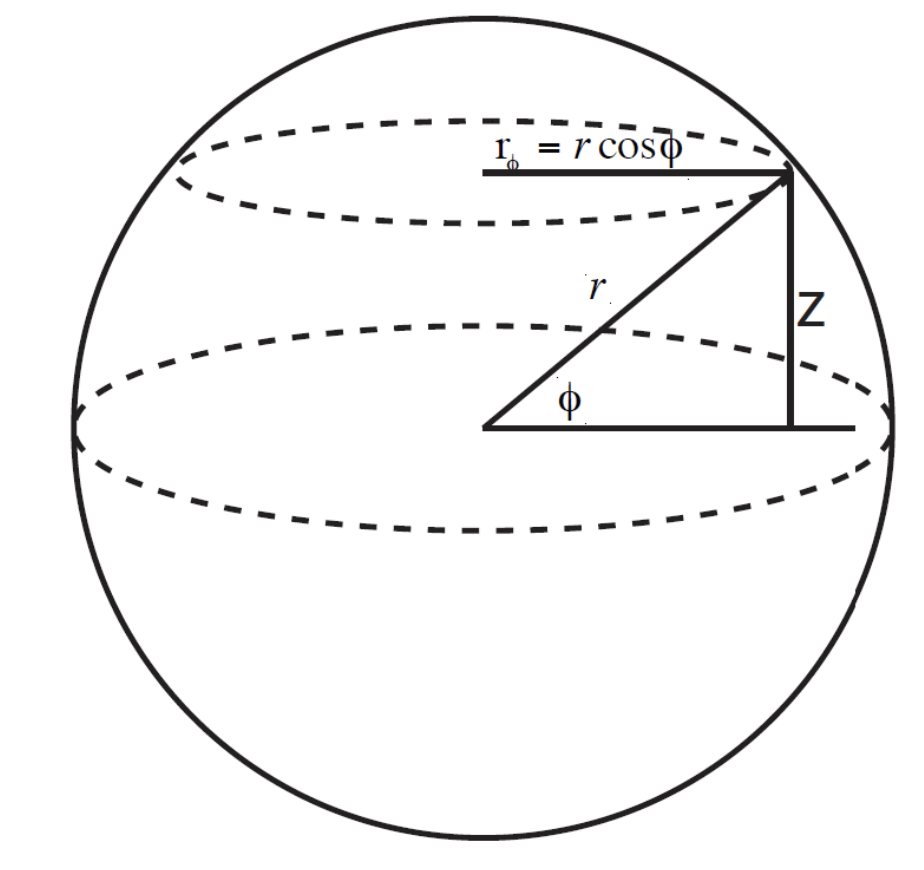
计算法线

为了让物体有明暗有质，你需要知道光线如何从表面反射 (reflecting light) 。法线 (Normal) 就是决定反射方向的向量。

对于一个 $p$ , $q$ , $r$ 三点定义的三角形，我们可以通过叉积 (Cross Product) 来计算法线：

获取两个边的向量： $u = q - p$ ， $v = r - p$
计算法线： $n = u \times v$
可选但推荐—— 标准化 (Normalize) 法线： $\hat{n} = \frac{n}{| n |}$

代码形式：

kotlin

fun normal(p: Point, q: Point, r: Point): Vector {
    val u = q - p
    val v = r - p
    
    val n = u.cross(v)
    val normalizedN = n / n.length 

    return normalizedN
}

为每个三角面计算并使用一个法线，此过程平面着色 (Flat Shading)，会使其看起来棱角分明。为了让近似的圆柱体/球体看起来平滑，我们不使用面法线，而是提供每个顶点 (per vertex) 的法线。

圆柱体：在某个顶点的法线，就是从圆心指向该顶点的水平向量 $(x, y, 0)$ 。
球体：对于一个中心在 $(0, 0, 0)$ 的球体，在表面任意一点 $(x, y, z)$ 的法线就是向量 $(x, y, z)$ 本身。

为什么点也能有法线？

你可能会疑惑，法线不是用来表示垂直于表面的方向吗，为什么点也能有法线？

这是因为，点法线 (Vertex Normal) 是专门为了服务于计算机图形学中的平滑着色 (Smooth Shading) 而“发明”出来的概念，在现实几何中没有意义，但在图形学中至关重要。

ppt 里没有介绍怎么利用法线，只是教了如何计算法线，以及它们可以做到什么。

Projective Rendering

投影渲染 vs 光线追踪

投影渲染 (Projective Rendering) 和光线追踪 (Ray Tracing) 是两种不同的图形渲染技术。

投影渲染：以物体为中心。为每个三角形，计算它在屏幕上的投影。
光线追踪：像素为中心。从每个像素出发，追踪光线与场景中物体的交点。更加复杂且消耗性能，但是能实现更逼真的光影效果。

遮挡

如果我们把所有三角形都投影到屏幕上，它们会产生遮挡 (Occlusion) 问题。需要一种手段，正确绘制三角形的前后关系。

画家算法 (Painter's Algorithm) 是一种简单的遮挡解决方案。它的核心思想是：从后往前绘制所有物体。但是该算法无法无法处理循环遮挡（ex：A 挡住 B，B 挡住 C，C 又挡住了 A）。

这是现代图形学的通常采用 Z-Buffering (深度缓冲) 作为解决方案，其核心在于：

开辟一块额外的内存 (Z-Buffer)，它与屏幕像素一一对应，但它存储的不是颜色，而是深度值 (z coordinate)。
当你要在 $(x, y)$ 处绘制一个新像素时，先计算它的深度 new_z。
检查 Z-Buffer 中 $(x, y)$ 位置的旧深度 old_z，只在 new_z 比 old_z 更靠近相机时，才绘制这个新像素，并更新Z-Buffer中的值为 new_z。

变换

变换参考 Games101 中内容，对于旋转部分你只要记住绕 X 轴、Y 轴、Z 轴的旋转矩阵即可：

我们此处重点讲解一下法线变换 (Normal Transformation) ——当物体经过变换 (Transformation) 后，法线也需要相应地变换，以确保光照计算的正确性。

我们依次考虑这四种情况：

平移
旋转
缩放
切变

对于平移，法线不变，因为平移不会改变表面的方向，这是很直观的；对于旋转和均匀缩放，法线可以直接使用相同的变换矩阵进行变换，因为旋转和均匀缩放不会改变表面的方向关系。

对于非均匀缩放，法线需要使用逆转置矩阵 (Inverse Transpose Matrix)。原因是，缩放会改变表面的方向，如果直接用缩放矩阵变换法线，会导致法线不再垂直于表面。使用逆转置矩阵可以确保法线在变换后仍然垂直于表面。

除了上述方法，你还可以在在缩放/切变之后，再重新计算法线，对于程序来说这其实是一种挺常见的做法。或者干脆避免使用缩放和切变也行。

Perspective Projection

文艺复兴时期的艺术家发现，现实世界中平行的线（如街道），在画面上并不是平行的，它们最后会它们汇聚在一个消失点 (Vanishing Point) 。

Orthographic Projection 平行投影

平行投影是一种简单的投影方式，它保持物体的比例和形状，但不考虑深度信息。所有的投影线都是平行的，因此不会产生消失点，也不存在近大远小。

那么，我们如何模拟近大远小的效果？我们通过相似三角形来做到这一点。

假设场景：

你的眼睛在原点 $(0, 0, 0)$ 。
成像平面（ppt 里称作 Image Plane）在 $z = d$ 处。
空间中有一个点 $P = (p_{x}, p_{y}, p_{z})$ 。

我们的目标是：计算 P 在成像平面上的投影点 $Q$ 的 $x$ 坐标，即 $q_{x}$ 。

眼睛成像

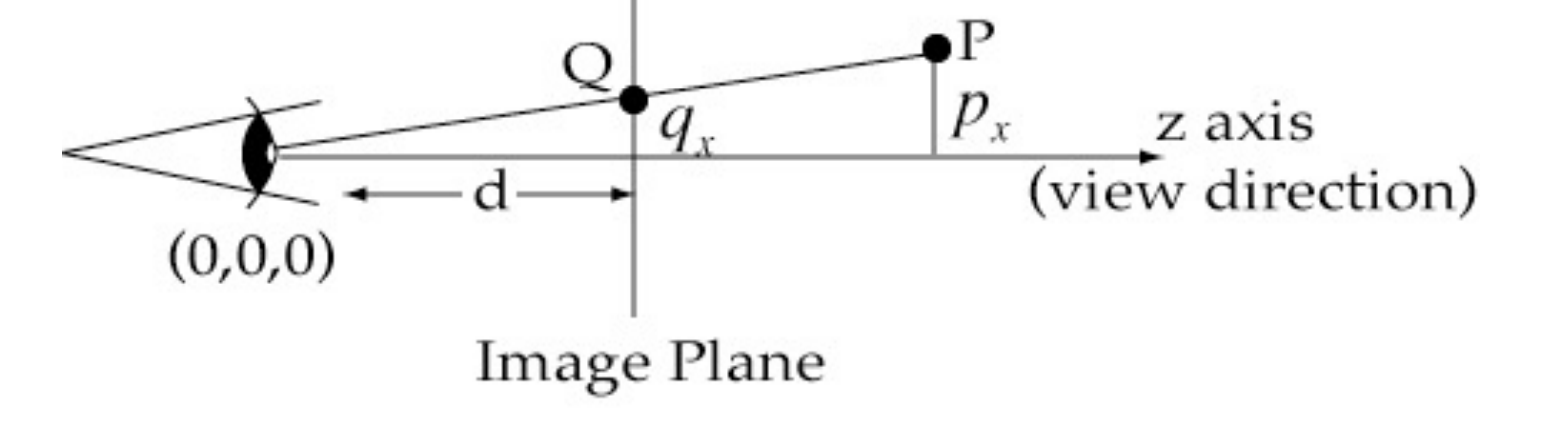
根据相似三角形的原理 $\frac{q_{x}}{d} = \frac{p_{x}}{p_{z}}$ ，我们有：

q_{x} = \frac{d \cdot p_{x}}{p_{z}}

可以得到结论： $q_{x}$ 与 $p_{x}$ 成正比， $q_{x}$ 与 $p_{z}$ 成反比。至此，我们成功地模拟出近大远小的效果。不仅如此，这种“除以 $Z$ ”的效应，会导致远处的物体不仅看起来更小，而且空间被压缩了，提供了纵深感。

Details

老师的 ppt 里没有介绍这一点，但我觉得说清楚有助于理解。

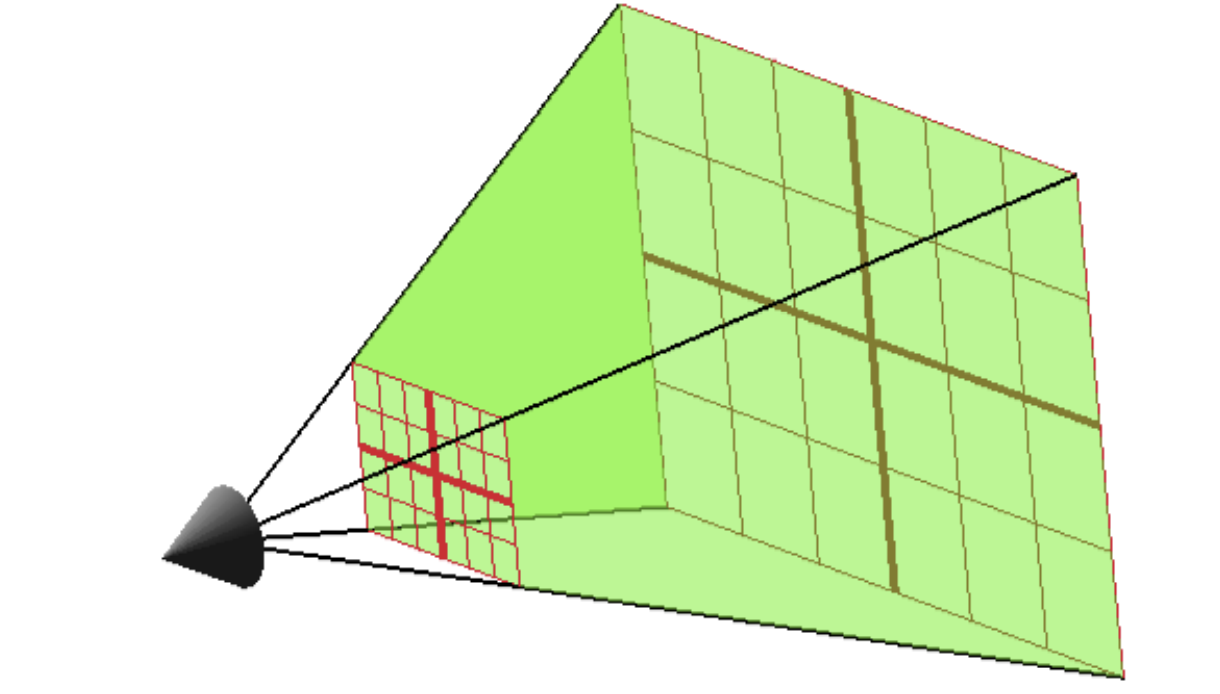
在现实世界中，光线穿过你眼睛的晶状体，晶状体（就像相机镜头）会把来自3D世界的、发散的光线聚焦，并清晰地成像在眼球后方的2D视网膜上。这个图像是倒立的，我们的大脑会再把它正过来。在图形学中，我们在眼前定义平面，这是为了方便计算，此外这个平面有个专门的名字——近平面 (Near Plane)。

人眼视野有限，于是我们也必须忽略太近或太远的物体。在透视投影中，我们能看到的空间是一个被切掉了顶部和底部的金字塔，该图形称为视锥体 (View Frustum) 。

Frustum

Projective Pipeline

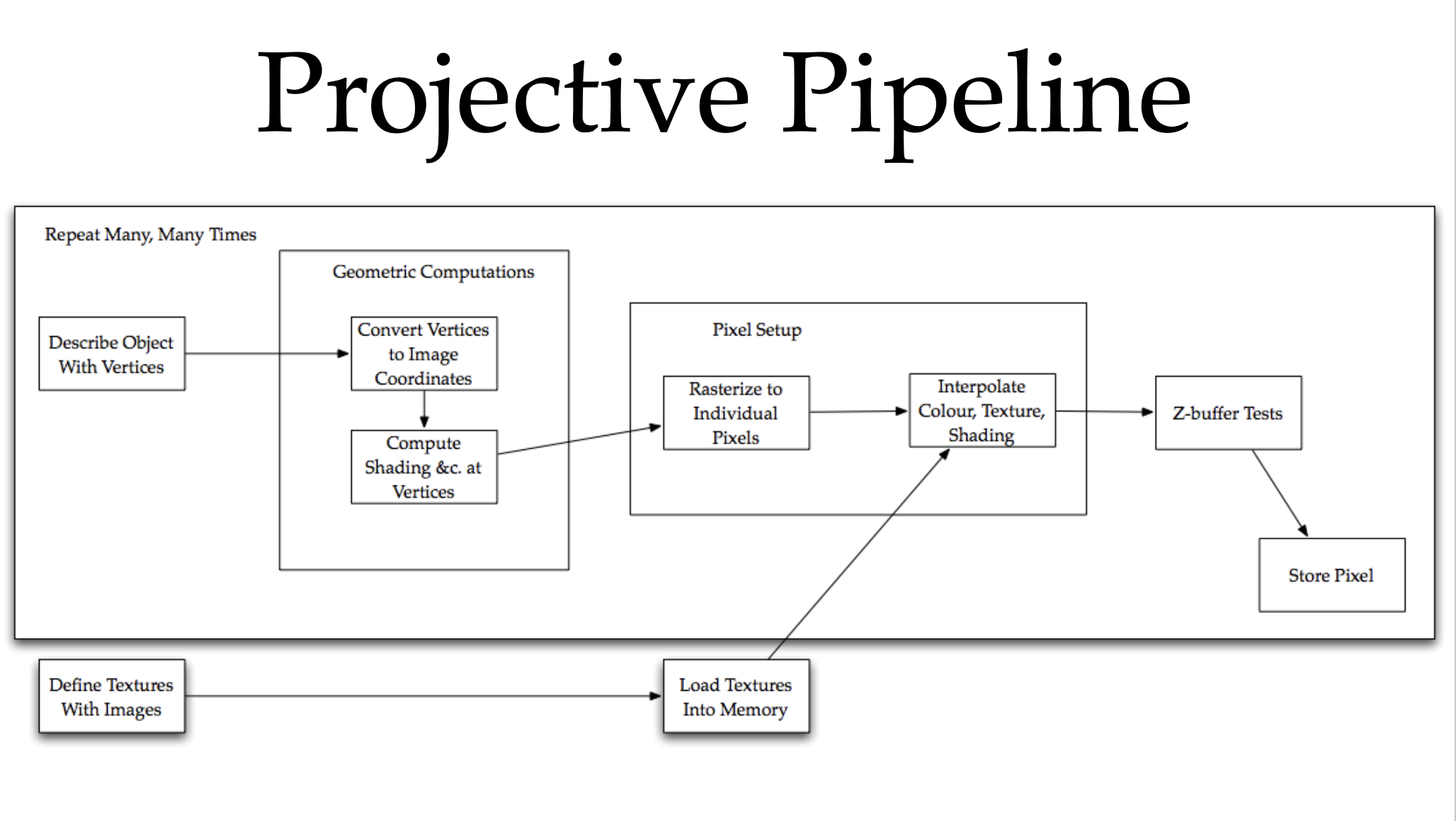
一个顶点从被建模出来到显示在屏幕上，会依次经过6个坐标系：

OCS (Object Coordinate System) - 物体坐标系
WCS (World Coordinate System) - 世界坐标系
VCS (View Coordinate System) - 视图坐标系
CCS (Clipping Coordinate System) - 裁剪坐标系
NDCS (Normalized Device Coordinate System) - 归一化设备坐标系
DCS (Device Coordinate System) - 设备坐标系

我们来一个一个看：

Model Matrix：OCS (物体坐标系) $\to$ WCS (世界坐标系)

起点：OCS 指的是物体本身的坐标系，原点在物体的中心。
终点：WCS 是一个全局坐标系，原点在场景的中心。
变换矩阵：Model Matrix，将物体从它的本地坐标系变换到世界坐标系。它通过平移、旋转和缩放，把物体放到场景中（OCS $\to$ WCS）。

View Matrix：WCS (世界坐标系) $\to$ VCS (视图坐标系)

起点：你的所有物体（树、房子）现在都已摆放在世界坐标系中。你的摄像机也在这个世界中，比如它在 $(50, 10, 5)$ 的位置。
终点 (VCS)：为了方便计算，我们不希望摄像机到处乱跑。我们希望摄像机永远固定在 $(0, 0, 0)$ 点，并且永远朝向 $Z$ 轴的负方向。
变换矩阵：View Matrix，它移动和旋转整个世界，使摄像机刚好落在 $(0, 0, 0)$ 并看向 $- Z$ 。你的摄像机不会动，而是整个世界在动。
TIP
摄像机看相的方向其实也是自身局部坐标系的 $- z$ 方向。

Projection Matrix：VCS (视图坐标系) $\to$ CCS (裁剪坐标系)

起点 (VCS)：现在，所有物体都在摄像机坐标系中。
终点 (CCS)：这是一个“扭曲”了的坐标系，也叫裁剪空间 (Clipping Space)。
变换矩阵：Projection Matrix 很复杂，它定义了摄像机的镜头属性，并将 Frustum 扭曲成一个立方体，以便后续处理。
1. 定义 View Frustum：根据你设置的 FOV (视野)、近平面 ( $z_{n}$ ) 和远平面 ( $z_{f}$ )，定义了一个金字塔形的可见空间。
2. 应用透视数学：它使用下方那个复杂的矩阵，把 Frustum 扭曲成一个规整的立方体。
3. 准备透视除法：在乘上下方的变换矩阵后，坐标 $(x, y, z, 1)$ 会变成 $(x_{c l i p}, y_{c l i p}, z_{c l i p}, - z)$ ，即 $w$ 分量携带了深度信息（ $- z$ ），为后续的透视除法做准备。

P = (\begin{matrix} \frac{1}{\tan (\frac{{FOV}_{x}}{2})} & 0 & 0 & 0 \\ 0 & \frac{1}{\tan (\frac{{FOV}_{y}}{2})} & 0 & 0 \\ 0 & 0 & \frac{z_{f} + z_{n}}{z_{n} - z_{f}} & \frac{2 z_{f} z_{n}}{z_{n} - z_{f}} \\ 0 & 0 & - 1 & 0 \end{matrix})

Perspective Division: CCS (裁剪坐标系) $\to$ NDCS (归一化设备坐标系)

起点 (VCS)：顶点还是齐次坐标 $(x, y, z, w)$ 。 $w$ 分量里携带着投影矩阵塞给它的深度信息。
终点 (CCS)：顶点变成了普通的3D笛卡尔坐标。
作用：通过这一步实现近大远小的效果。我们通过除以 $w$ 分量，来实现透视投影的“除以 $Z$ ”效应：

x_{n d c} = \frac{x}{w}, y_{n d c} = \frac{y}{w}, z_{n d c} = \frac{z}{w}

Viewport Transformation: NDCS (归一化设备坐标系) $\to$ DCS (设备坐标系)

起点 (NDCS)：经过先前的步骤，所有可见的坐标最后都会被压缩到一个与屏幕大小无关的、标准的立方体（如 $- 1$ 到 $1$ ）中。
终点 (DCS)：将所有顶点从标准立方体映射到实际的屏幕像素坐标系里。
作用：把那个归一化的坐标拉伸，以匹配你实际的窗口大小。比如将 $(- 1, - 1)$ 映射到屏幕的左下角 $(0, 0)$ ，将 $(1, 1)$ 映射到屏幕的右上角 $(1920, 1080)$ 。
TIP
这一步是渲染和操作系统 (O/S) 窗口的桥梁。当你的窗口被重设大小 (resized) 时，只有这个变换需要被更新。

Projective Pipeline 总结图

Projective-Pipline

OpenGL 的投影渲染管线

OpenGL 是一个强大的图形库，我们来学习使用它。

基本绘图命令

glBegin(mode)：在发送顶点数据之前，指定 mode 来告诉 GPU 如何理解这些顶点数据。常见的 mode 有：
- GL_POINTS：每个顶点都是一个独立的点。
- GL_LINES：你发的每两个顶点，都会被连接成一条线段。
- GL_TRIANGLES：你发的每三个顶点，都组合成一个三角形。
glEnd()：标记顶点数据的结束。

在 glBegin 和 glEnd 之间，你不仅要发顶点的位置，还要发它的属性（法线、颜色等）。OpenGL 本身是一个状态机 (State Machine)，这意味着你设置的一个属性（比如“当前颜色设为红色”）会一直保持（hangs around），直到你再次更改它。

java

// 开始绘制三角形
glBegin(GL_TRIANGLES); 

// 设置颜色为红色
glColor3f(1.0, 0.0, 0.0);
glVertex3f(x1, y1, z1);
glVertex3f(x2, y2, z2);
// 设置颜色为绿色
glColor3f(0.0, 1.0, 0.0);
glVertex3f(x3, y3, z3);

// 结束绘制
glEnd();

OpenGL 要求你先设置好一个顶点的所有属性，最后才用 glVertex() 来提交这个顶点。调用顺讯：

glNormal(...)：设置当前的法线状态。
glColor(...)：设置当前的颜色状态。
glTexCoord(...)：设置当前的纹理坐标状态。
glVertex(...)：（最后一步）设置位置坐标，并且把刚才设置的‘当前’法线、颜色、纹理全都打包给这个顶点。

java

// --- 绘制顶部(绿色)三角形的第一个顶点 ---
glNormal3f(x1, y1, 0.0);    // 1. 设置法线
glVertex3f(x1, y1, 0.0);  // 2. 提交顶点 (这个点打包了上面的法线)

// --- 绘制顶部(绿色)三角形的第二个顶点 ---
glNormal3f(x2, y2, 0.0);    // 1. 设置新的法线
glVertex3f(x2, y2, 1.0);  // 2. 提交顶点 (这个点打包了新的法线)

// --- 绘制顶部(绿色)三角形的第三个顶点 ---
glNormal3f(x1, y1, 0.0);    // 1. 再次设置法线
glVertex3f(x1, y1, 1.0);  // 2. 提交顶点 (这个点打包了这条法线)

平滑着色 (Smooth Shading)：当你设置 glShadeModel(GL_SMOOTH)，GPU 会拿走这三个顶点的属性（比如一个红、一个绿、一个蓝），然后在光栅化时，使用重心坐标在三角形内部进行插值 (interpolate)。
平面着色 (Flat Shading)：当你设置 glShadeModel(GL_FLAT)，GPU 会简单地只用第一个顶点的属性来填充整个三角形。

矩阵、变换与摄像机

OpenGL 做了一个简化：它只提供了两个主要的矩阵栈：

GL_PROJECTION (投影矩阵)：
- 用途：专门用来存放 Projection 矩阵。
- 对应管线： VCS $\to$ CCS
GL_MODELVIEW (模型视图矩阵)：
- 用途：这是一个合并的矩阵。它同时存放 Model 矩阵和 View 矩阵。
- 对应管线： OCS $\to$ WCS $\to$ VCS

因为只有两个矩阵栈，你必须明确告诉 OpenGL 你接下来要操作的是哪一个：

java

glMatrixMode(GL_PROJECTION); // 选择投影矩阵栈
// ...
glMatrixMode(GL_MODELVIEW);  // 选择模型视图矩阵栈
// ...

在设置摄像机时，你需要先设置 View 矩阵，然后再设置 Model 矩阵。你不需要自己计算。使用辅助库 GLU：

java

// eye：你的摄像机在世界中的位置
// center：你的摄像机正在看向的目标点
// up：摄像机的头顶朝向哪个方向（通常是 (0, 1, 0)）
GLU.gluLookAt(eyex, eyey, eyez, centerx, centery, centerz, upx, upy, upz);

设置镜头：

java

// 切换模式
glMatrixMode(GL_PROJECTION); 
// 重置矩阵
glLoadIdentity();

// 选择你的“镜头”：

// 透视投影 (Perspective)：
// fovy：Y轴的视野角度（Field of View），单位是度 。
// aspect：宽高比（width/height），用来防止图像被拉伸 。
// zNear / zFar：近/远裁剪平面。
gluPerspective(fovy, aspect, zNear, zFar);
// 非对称视锥体：glFrustum(left, right, bottom, top, zNear, zFar);

// 正交投影 (Orthographic)：
glOrtho(left, right, bottom, top, zNear, zFar);

操作物体 (Model Matrix)：

java

// 切换模式
glMatrixMode(GL_MODELVIEW);
// 重置矩阵
glLoadIdentity();
// 设置摄像机
gluLookAt(...);
// 现在开始操作物体
// 这些函数会把新的变换矩阵乘到当前矩阵上（glMultMatrix）。
// 因为是“后乘”，所以执行顺序是反的。
glTranslate(...);
glScale(...);
glRotate(angle, x, y, z);

管线的最后一步——设置视口：

java

// 设置视口 (Viewport)
glViewport(0, 0, windowWidth, windowHeight);

设置光照与着色

打开光照，你可以设置多个光源：

java

glEnable(GL_LIGHTING); // 启用光照计算
glEnable(GL_LIGHT0);   // 启用第0号光源

配置光照属性：

java

// 设置光源位置
float[] lightPos = {x, y, z, w}; // w=1.0 表示点光源，w=0.0 表示方向光
glLightfv(GL_LIGHT0, GL_POSITION, lightPos, 0);
// 设置光源颜色
float[] lightColor = {r, g, b, a};
glLightfv(GL_LIGHT0, GL_DIFFUSE, lightColor, 0);
// 设置环境光颜色
float[] ambientColor = {r, g, b, a};
glLightfv(GL_LIGHT0, GL_AMBIENT, ambientColor, 0);
// 设置镜面反射颜色
float[] specularColor = {r, g, b, a};
glLightfv(GL_LIGHT0, GL_SPECULAR, specularColor, 0);

当开启光照后，getColor() 函数将不再生效，取而代之的是材质函数 glMaterial()：

java

float[] matDiffuse = {r, g, b, a};
glMaterialfv(GL_FRONT, GL_DIFFUSE, matDiffuse, 0);

一个完整的流程

java

// 只需设置一次
void Start() {
    // 设置镜头
    glMatrixMode(GL_PROJECTION); 
    glLoadIdentity();
    gluPerspective(fovy, aspect, zNear, zFar); // 透视投影
    // 设置视口
    glViewport(0, 0, windowWidth, windowHeight);
}

// 每一帧都要设置
void Update() {
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); // 清屏
    glMatrixMode(GL_MODELVIEW);
    glLoadIdentity();
    // 设置摄像机
    gluLookAt(
        0.0f, 0.0f, 5.0f,  // eye position
        0.0f, 0.0f, 0.0f,  // look at point
        0.0f, 1.0f, 0.0f   // up vector
    );
    // 绘制物体
    glBegin(GL_TRIANGLES);
        // 设置顶点属性并提交顶点
        glNormal3f(...); 
        glColor3f(...);  
        glVertex3f(...); 
    glEnd();
}

Texture

纹理就是一张“画” ，被“贴”在一个3D模型的表面上。如果说之前的内容是在定义物体的几何形状，那么纹理就是在定义物体的外观细节。

组成纹理图像的像素被称为 Texel (纹理像素) 。要将一张贴图贴在3D模型上，我们需要一种映射关系，将材质上的每个 Texel 对应到模型表面的一个点。为了方便地描述这种关系，我们为 3D 模型表面定义一个2D坐标系，用 $(s, t)$ 表示，2D 纹理像素坐标用 $(i, j)$ 表示。

我们从一个把世界地图贴在球体上的例子开始：

我们有一个在球面上的3D顶点 $(x, y, z)$ ，将其转换为球坐标（经纬度） $(ϕ, θ)$ ：

ϕ = \arcsin (\frac{z}{r})

θ = \arctan 2 (y, x)

在 OpenGL 里，纹理坐标 $(s, t)$ 的范围是 $[0, 1]$ ，故我们也需要将球坐标限制在这个范围内：

s = \frac{ϕ + \frac{π}{2}}{π}

t = \frac{θ + π}{2 π}

在 OpenGL 里，提供了 glTexCoord2f(s, t) 函数来设置当前顶点的纹理坐标。你需要在 glVertex() 之前调用它：

kotlin

for (theta in 0 until numTheta) {
    for (phi in 0 until numPhi) {
        // 1. 计算顶点位置
        val x = r * cos(phi) * cos(theta)
        val y = r * cos(phi) * sin(theta)
        val z = r * sin(phi)

        // 我们在这里“预先”把 (phi, theta) 转换成 (s, t)
        val s = (phi + Math.PI / 2) / Math.PI
        val t = (theta + Math.PI) / (2 * Math.PI)

        // 3. 把预计算好的 (s, t) 发送给GPU
        glTexCoord2f(s, t)    
        glVertex3f(x, y, z)
    }
}

$(s, t)$ 坐标超出了 $[0, 1]$ 范围怎么处理？

Clamping (钳位)：将超出范围的坐标限制在 $[0, 1]$ 内，大于 $1$ 的部分设为 $1$ ，小于 $0$ 的部分设为 $0$ 。
Repeating (重复)：将坐标对 $1$ 取模，使其在 $[0, 1]$ 范围内循环，如此可以实现平铺效果。

java

// Clamping
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
// Repeating
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT);

$(s, t)$ 算出的 $(i, j)$ 不是整数字怎么办？

Nearest Neighbour：将 $(i, j)$ 四舍五入到最近的 texel。放大观察时可能产生马赛克。
Bilinear Interpolation (双线性插值)：同时读取周围4个 texel，然后根据距离远近做加权平均。这是一个两步插值——先在 $X$ 方向（水平）做两次插值，再在 $Y$ 方向（垂直）对刚才的结果做一次插值。图像更平滑，但会模糊边缘。

java

// Nearest Neighbour
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
// Bilinear Interpolation
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);

如何使用纹理颜色？

Replace (替换): 完全忽略光照计算。物体是“自发光”的。无论有没有灯光，地球仪都是亮的。
Modulate (调制): 把纹理颜色和光照计算结果（dot(N, L)）相乘。纹理会受到光照的影响。

java

// Replace
glTexEnvf(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_REPLACE);
// Modulate
glTexEnvf(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_MODULATE);

纹理矩阵

通过纹理矩阵 (Texture Matrix)，你可以对纹理坐标进行变换（平移、旋转、缩放），从而实现动态纹理效果，而不需要修改顶点数据本身。

北工大图形学 ​

Introduction ​

Linear Algebra ​

Rasterization ​

线 ​

填充三角形 ​

Geometric Modelling ​

描述世界 ​

万物皆为三角形 ​

计算法线 ​

Projective Rendering ​

投影渲染 vs 光线追踪 ​

遮挡 ​

变换 ​

Perspective Projection ​

Projective Pipeline ​

OpenGL 的投影渲染管线 ​

基本绘图命令 ​

矩阵、变换与摄像机 ​

设置光照与着色 ​

Texture ​

北工大图形学

Introduction

Linear Algebra

Rasterization

线

填充三角形

Geometric Modelling

描述世界

万物皆为三角形

计算法线

Projective Rendering

投影渲染 vs 光线追踪

遮挡

变换

Perspective Projection

Projective Pipeline

OpenGL 的投影渲染管线

基本绘图命令

矩阵、变换与摄像机

设置光照与着色

Texture